Solution
The specific answer to Problem 1188 is just a little over 3 cm. It was solved by John Guilford, Franz Pilcher, Joseph DeVincentis, Stephen Dupal, Barry Cox, and Michael Elgersma. One incorrect solution was received.
A beautiful aspect of the problem is that the center of mass, when at its minimum, lies on the upper surface of the water. A paper about this result is by Marie Baehr: "Center of mass of a can with a varying level of liquid," The Physics Teacher, 30 (Jan 1992) 34-36.
The reason for this is: If the center of gravity is on the water surface and water is added, that must increase the overall center of gravity. If water is subtracted, look at the region of removed water. Its center of gravity is below the original, so its removal must raise the center of gravity.
This idea can be used to solve the problem efficiently by setting the center of mass equal to the height of water and solving. Barry Cox did this as:
z == ((1/2) d π r² z² + (1/2) h C) / ( C + d π r² z)
This is a quadratic equation easily solved for z. Here, z is the height of the water. C is the mass of the can. r is the radius of the can. h is the height of the can, and d is the density of the liquid. This method avoids calculus.
The more common method is to set this up as a calculus problem and take the derivative w.r.t. z. One can use the expression above (right side of equation), or start from scratch, as done in Guilford's solution, below.
Let m1 be the mass of the can, let m2 be the mass of the water in a can full of water, let the can be one unit high, and let x be the level of water in the can (how full it is).
The center of mass of the (empty) can is 1/2. The mass of the water is x * m2. Its center of mass is at x/2.
The combined center of mass is
[m1*1/2 + (x*m2)*(x/2)]/2[m1 + x*m2]
= 1/2 * (m1 + x²*m2)/(m1 + x*m2).
Note that for both x = 0 (empty can) and x = 1 (full can), the center of mass is at 0.5, as expected.
The lowest value for the center of mass is found by differentiating and setting to zero. This results in the equation
x²m2² + 2m1m2x − m1m2 = 0
This has the positive solution at
x = [-m1 + √(m1² + m1m2)]/m2.
For your numbers, m1 = 50 g. The volume of the can is
π * 3.5² * 13 = 500.3 = m2
For these numbers, the optimum is at
(-50 + √(50² + 50*500))/500 = 0.23 units, or 3 cm.
It is easy to see that, for this case, the tipping angle (where 0 is vertical) is π/2 − arctan(3/3.5) = 49.4°.
Now, several of you pointed out that for the more true-to-life problem of maximizing the stability of the can, the version above is inadequate. There is the fact that water will slosh around, but we will not address that. More important is that the water will move so that the top surface stays horizontal, and this changes the angle at which the can will tip.
Using Mathematica's ability to evaluate triple integrals based on a Boolean function and inequalities to define the regions in question, I worked out that, for the given sizes, the optimal water height is 3.9 cm, leading to a critical angle of 41.8°. A figure showing the situation is at
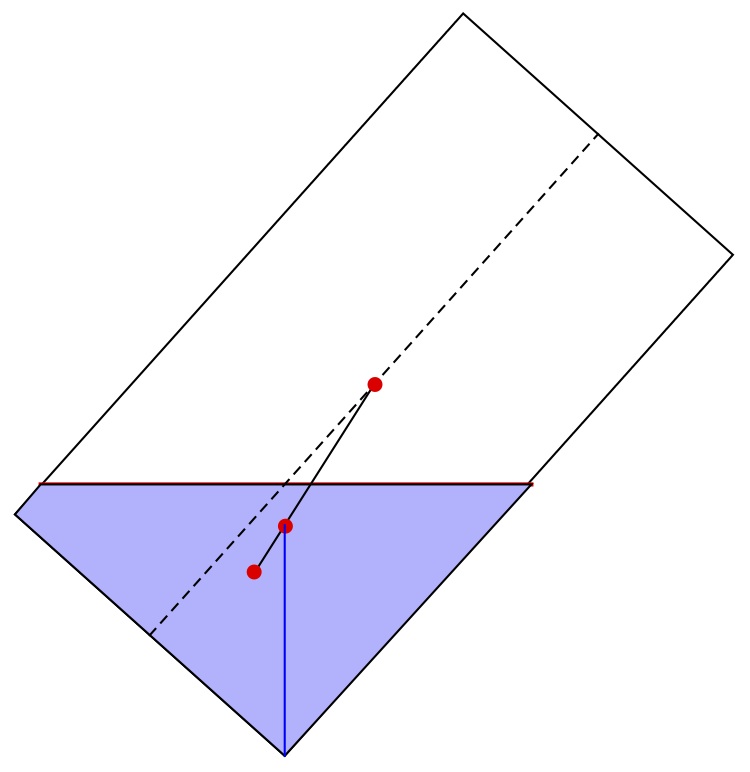
Michael Elgersma, approaching the problem a little differently, got the same result: 3.912 cm and 41.82°. His work is more symbolic.
[Back to Problem 1188]
© Copyright 2014 Stan Wagon. Reproduced with permission.