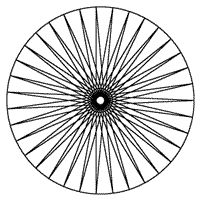
Alice: Check out this nifty new virtual dartboard I made. It's a star
with 35 spikes contained in a unit circle. Let's play a game where the
computer throws a dart randomly at the round board. If it lands outside the
star-shaped region I win, otherwise you win.
Bob: No fair! Your region clearly has more than half the area. I'll play if you
give me 2:1 odds.
Should Alice accept?
Note: To get a 35-spiked star place 35 points uniformly around a unit circle, starting at (1, 0), and number them counterclockwise as 1, 2, 3,..., 35. Then the star is obtained by connecting 1, 18, 35, 17, 34, 16, 33, 15, 32, 14, 31, 13, 30, 12, 29, 11, 28, 10, 27, 9, 26, 8, 25, 7, 24, 6, 23, 5, 22, 4, 21, 3, 20, 2, 19, 1. In short, each vertex connects to the two vertices that are farthest from it.
Enthusiasts: Generalize to any regular star with an odd number of spikes.
By the way, Ramshaw thought of this problem while thinking about the famous Kakeya needle problem, which many of you will know has to do with a region of small area that is large enough to turn a needle around in.
© Copyright 1998 Stan Wagon. Reproduced with permission.