On April 1, 1975, Martin Gardner, editor for many years of the Mathematical Games column in Scientific American, published a map with a claim that it required five colors if adjacent countries were to receive distinct colors. This was just a hoax, however, and in 1976 the four-color theorem was proved. [A simpler proof was announced by Robertson, Sanders, Seymour, and Thomas in 1996 and published in 1997. -Jeff]
Here is the April Fool's map, with a few twists to make its coloring harder. Can you 4-color it? For an extra challenge consider the exterior "ocean" as an additional country and assign it one of the four colors too.
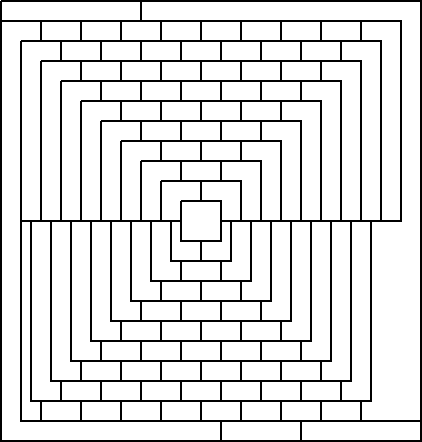
[A postscript version of the map is also available. -Jeff]
Misc. notes from the past year:
It seems that my main academic efforts this past year had to do with
the four-color problem. I programmed a routine in Mathematica that
will succeed in 4-coloring any planar graph (well, whether it
always works is open, for an affirmative answer would yield a
proof of the 4CT; but it works well in practice). The ideas are not
wholly original, as they are simply a straightforward implementation
of the ideas of Kempe's false proof of 1879, together with an
interesting modification due to
Most recently I have upgraded my package so that it can take a map and produce the corresponding planar graph drawn in such a way that each edge stays entirely within the countries it connects. This is a nontrivial geometrical problem if the countries are highly nonconvex. Using this routine one can, for example, take the map of this week's problem, turn it into a graph, and 4-color it. It is not so easy to do that by hand (I think).
© Copyright 1997 Stan Wagon. Reproduced with permission.