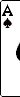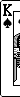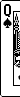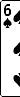Problem of the Week 825

Poker Hands

Rank the following poker hands from best to worst. The game is being played with an ordinary 52-card deck, and there are no wild cards.

1. 
2. 
3. 
4. 
5. 

(For people with non-graphical browers: S=spades, H= hearts, D=diamonds, C=clubs, A=ace, K=king, Q=queen)

Source: A.J. Friedland, Puzzles in Math & Logic, Dover (1970).

---

Here is a summary of poker hand rankings from high to low. For an explanation of each, visit http://www.contrib.andrew.cmu.edu/org/gc00/reviews/pokerrules

1. Straight Flush
2. Four of a Kind
3. Full House
4. Flush
5. Straight
6. Three of a Kind
7. Two Pair
8. Pair
9. High Card

Ties are broken by high cards. To answer all those questions: yes, the problem is more subtle than simply saying that the first hand beats all of the others.
Playing card images taken (with permission) from oxymoron's Egyptian Ratscrew page.

---

See Jeff Erickson's solution.

© Copyright 1996 Stan Wagon. Reproduced with permission.