Problem of the Week 1176

Unique Addresses

Let X be a set of points in the plane. For any point P in X and integer m, let L(m)(P) be the number of lines through P that contain exactly m points of X.

Then the "address" of P is defined to be the sequence:

L(3)(P), L(4)(P), L(5)(P), ....

Find a finite set of at least two points such that the set of addresses of the points has no duplicates.

For a sample configuration with addresses attached, see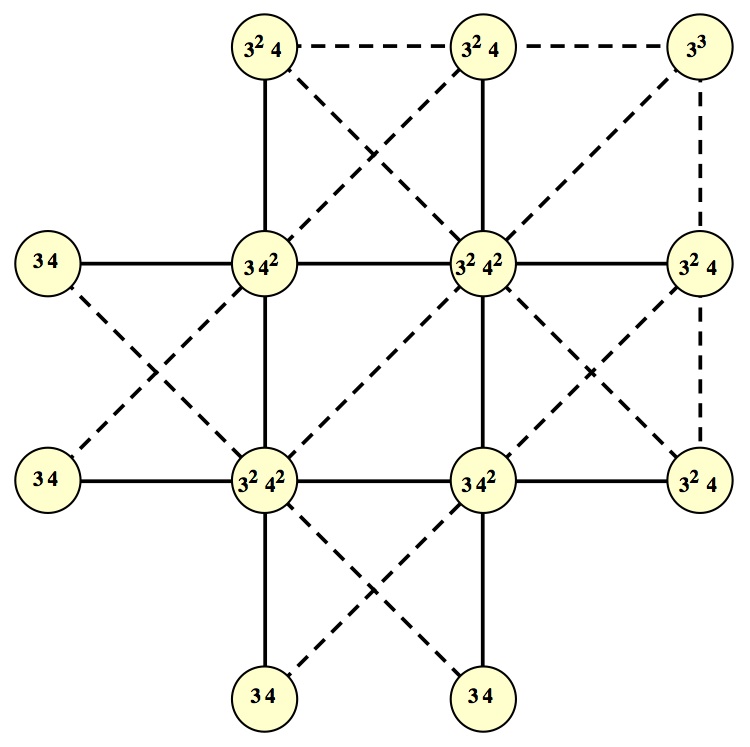

It is convenient to write addresses by exponents. For example, the address (0, 3, 0, 2) is 4³ 6².

Comments: The best result known is that such a set exists having size 16. Proposer Gary Gordon and I wonder if any reader can find a smaller set. If you wish to see the configuration for 16, just ask me.

There is no loss of generality in restricting to integer points, since all intersections of lines determined by such points are rational.

A related, but simpler, problem is: Find an infinite set of points in the plane so that all the addresses are distinct.

Source: Due to Gary Gordon (Lafayette College); appeared in Math Horizons, Sept. 2013.

© Copyright 2014 Stan Wagon. Reproduced with permission.

[View the solution]