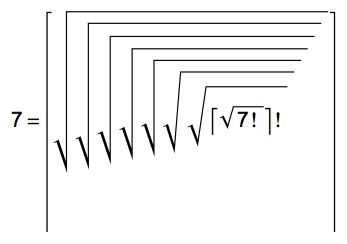
Problem of the Week 1171

Four Unary Functions

Call n, a positive integer, "good" if one can start with n and use the operations factorial, square root, floor and ceiling to obtain n, using at least one of the first two operations.

For example, 7 is good because Ceiling[Sqrt[7!]]! after extracting 7 square roots gives 6.3, and so a final ceiling gives 7:

Show that n is good for all n ≤ K, where K is as large as you can get.

Note: Here, factorial can operate only on integers. So while the example above, using the gamma function, works using Sqrt[7!]! instead of Ceiling[Sqrt[7!]]!, that is not legal. The assertion that all positive integers are good is a conjecture of Don Knuth and Richard Hess.

Note that the actual representations are not sought, just the proof that the representation exists. It has been conjectured by D. Knuth and R. Hess that all positive integers are good.

Source: Crux Math, M506, 38:8 Oct 2012, 310-313.

© Copyright 2013 Stan Wagon. Reproduced with permission.

[View the solution]