Problem of the Week 1166

The Hex Queen

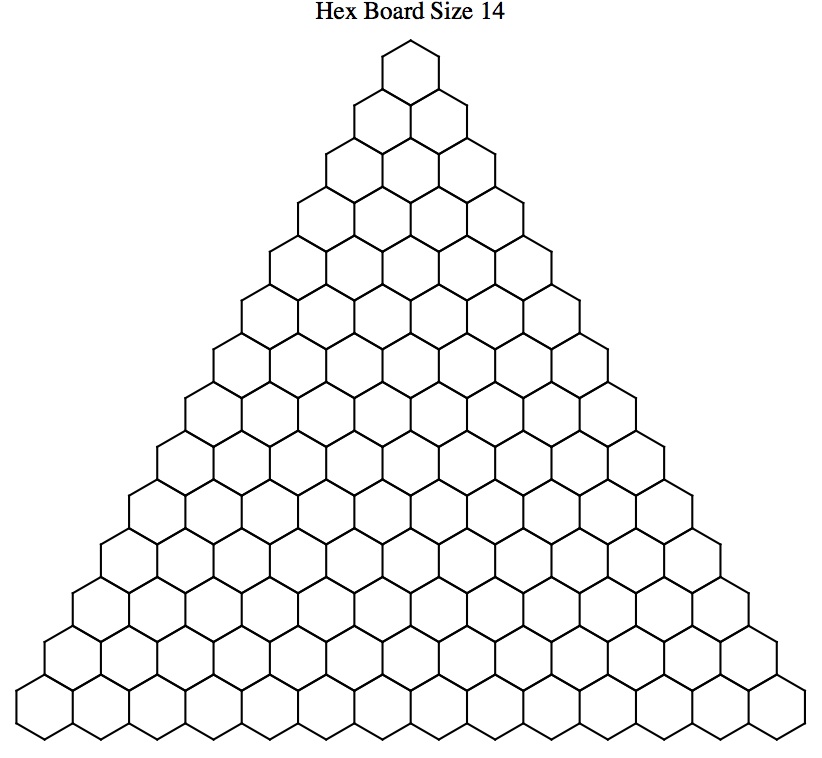
A hex board H(n) is a triangular board using hexagonal cells, with n cells on a side:

A hex queen can move along a row of adjacent cells in any of the three directions.

What is the smallest number of colors that can be assigned to the cells of H(14) so that attacking queens get different colors?

Source: Dan Ullman and Stan Wagon.

More: This problem seeks the chromatic number of HQ(14), the HexQueen graph on the 14-board. One wants to know more HQ parameters, and for all n.

Here is a brief summary of what is and is not known for queens (there are also kings, bishops, and knights that are worthy of study).

Hex Queen Summary:

regular: yes, degree d = 2n − 2.
chromatic number: known for all n.
fractional chromatic number: known for all n.
independence number: known for all n; it is Floor[(2n + 1)/3)].
largest clique and clique covering number are both, trivially, n.
domination number, g (as in the classic problem of placing standard chess queens on a board so as to attack all squares, to which the answer is 5):

For n even, the central vertical line of cells is a simple dominating set of size n/2. For n odd, one can move n up by two using the apex of the new graph to dominate the two new long diagonals. Because g(1) = 1, this gives g(3) = 2 and g(5) = 3, all optimal. But a miracle happens at 7, and g(7) is 3; it is a nice exercise (very old PoW) to find the three queens that dominate H(7). Moving up from there by choosing the apex of the larger graph gives g(9) = 4, g(11) = 5, and so on through all odds. But proving that these are optimal is an unsolved problem, except for n up to 17, where I proved optimality using integer-linear programming. So one wonders whether another miracle similar to n = 7 ever happens (as some think might be possible) or whether the formula Floor[n/2] is valid for all n beyond 7 (which I think is true).

Update: Rob Pratt (SAS), using his integer-linear programming methods, found that a "miracle" does happen at n = 20, and that HexQueen is coverable by less than 10 vertices:

So we can move up from here, thus concluding that for evens past 20, gamma is under n/2 by one. Presumably there are other such "miracles" in addition to 7 and 20. It would be nice to know another odd miracle....

edge chromatic number:

A regular graph with vertex count that is odd and at least 3 is never class 1, so that settles n = 2, 5, 6, 9, 10, 13, 14, ... in the negative. The others (3, 4, 7, 8, 11, 12, 15, 16, ...) appear to be class 1, i.e., have edge-chromatic number equal to the max degree. Computations using a Vizing-Kempe algorithm show that this is correct up to n = 32. General proof lacking. Last time this sort of problem came up in the PoW, Joseph DeVincentis proved that the standard queen graph Q(m,n) is class 1 if one of m, n is even or if m = n is odd; possibly similar techniques would work here.

Hamiltonian: easy
Hamiltonian decomposition: appear to exist in all cases (and this implies the class 1 conjecture above).

For more, see Wikipedia. The pieces in true hexagonal chess are defined differently than I have done here. In particular, what is called a Hex Queen here is really a rook in the chess game. Mathematically, it seems that the true hexagonal chess pieces for king, bishop, and queen are not as interesting as the variants, since they do have nice geometric definitions. For example, one could consider a geometric kingas using nearest neighbors only; that graph is somewhat well studied and knownas the triangular grid graph. So from this point of view, the rook is the onlyone of the traditional hex chess pieces with a nice adjacency definition, and this problem probably should call the object of study the hex rook graph, as opposed to the hex queen graph.

[View the solution]

2 October 2013