Problem of the Week 1165
Self-Replicating Resistors
Thanks to some good work by POW reader Brian Trial (Ferndale, Mich.) we now have a complete, and rather surprising solution to this problem. The bottom line is that there is an essentially unique integer solution.
There are three variations: the "very hard version" is quite difficult and requires a lot of computer work. The "medium hard version" was also done by computer, but it is possible there is a solution by hand, so I will take that as the main Problem 1165. If you solve this by hand, let me know. The third gives more info, and can be done by hand fairly easily.
Background: You will need to know that the resisitance of x and y in series is x + y, and in parallel is 1/(1/x + 1/y).
|
Very Hard Version
|
|
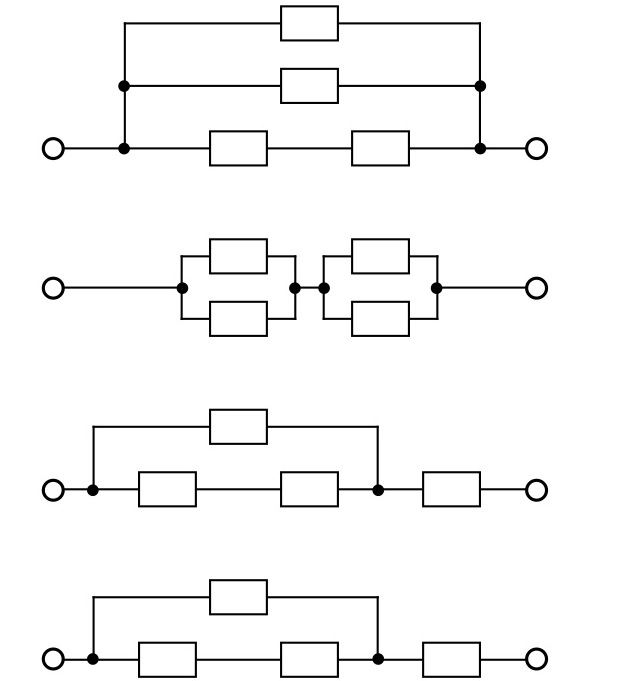
Suppose positive integers a < b < c < d are the values of four resistors that form a self-replicating set. There are four networks, each of which consists of the four resistors a, b, c, d used once and only once, their resistance values being a, b, c, d.
What are the possible values of a, b, c, d?
The point here is that: (a) there is an integer solution, and (b) it is essentially unique.
|
|
Medium Hard Version
|
|
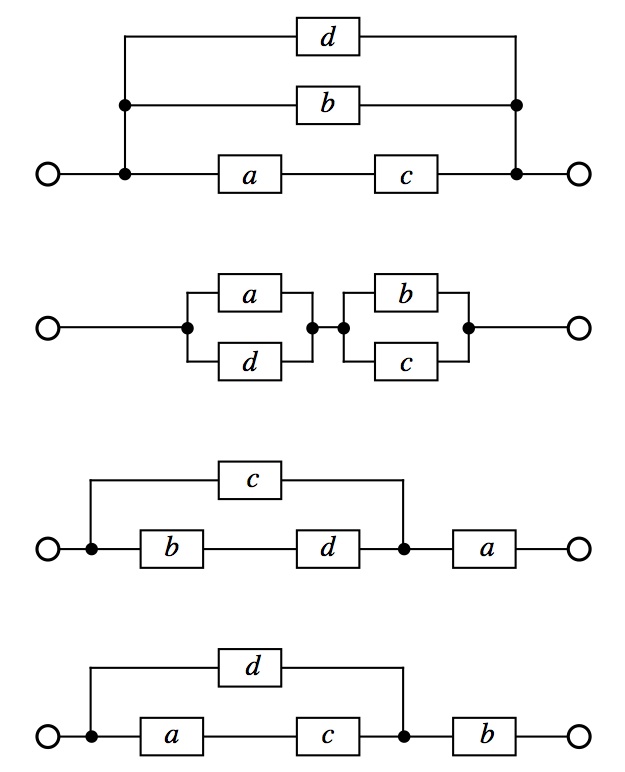
Each of the four networks shown in the diagram, right, uses the same four distinct integer-valued resistors a, b, c, d, and the total resistances of the networks themselves are again a, b, c, d.
Find values of a, b, c, d that work, with a being as small as possible.
|
|
|
Easy Version
|
|
Find distinct integer values of the resistors at a, b, c, d in the diagram, right, so that the total resistances of the four networks shown are a, b, c, d.
|
|
Source: Lee Sallows, Brian Trial, and Stan Wagon.
© Copyright 2013 Stan Wagon. Reproduced with permission.
[View the solution]
|

