Problem of the Week 1148

Seamless Brickwork

The diagram below shows a special arrangement of three rows of four bricks each:

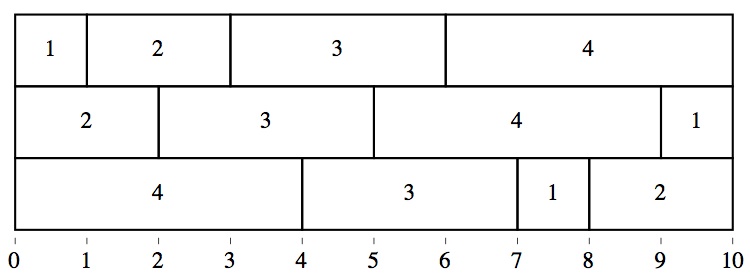
In each row, the size is a permutation of (1, 2, 3, 4). Moreover, the arrangement is such that no two of the vertical dividers between bricks is aligned. In other words, each of the 9 partial sums 1, 2, 3, 4, 5, 6, 7, 8, 9 arises once and once only when the sums along each row are formed. Three rows are used because, ignoring the ever-present terminal sum of 10, each row contributes three partial sums, for a total of 9.

Find such an arrangement using 1, 2, 3, 4, 5, 6 in each row. The possible sums are then 1, 2, 3, 4, ..., 20 and each row contributes five, so one needs four rows.

This problem makes sense for any even n = 2k, but I am not aware of the current best-known results. Does anyone know? Because the total number of sums is n(n + 1)/2 − 1 and each row contributes n − 1 sums, the number of rows is k + 1. Thanks to Rob Pratt using sophisticated compuational methods, I can say that there are solutions for n = 4, 6, 8, 10, 12, 14, 16, 20, 22, 24, 26, 30, 34, 38.

Source: Suggested by Tom Halverson who heard it in a recent lecture by Barry Cipra.

© Copyright 2011 Stan Wagon. Reproduced with permission.