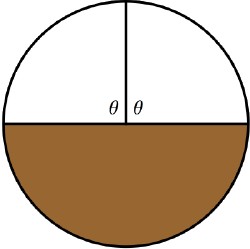
Problem of the Week 1101It's a Piece of CakeA round cake has icing on the top but not the bottom. Cut out a piece in the usual shape (sector of a circle with vertex at the center), pull it out, turn it upside down, and replace it in the cake to restore roundness. Do the same with the next piece; i.e., take a second piece with the same vertex angle, but rotated counterclockwise from the first one so that one boundary edge coincides with a boundary edge of the first piece. Remove it, flip it, and replace it. Keep doing this in a counterclockwise direction. This diagram shows what happens after two moves in the case that the central angle is a right angle.
For some central angles what happens is clear. For a 90° angle it takes eight moves for all the icing to return to the top. If the angle is 180°, it takes four moves to return to the initial state. Suppose the central angle is 181°. When does all the icing first return to the top? Extra credit: What happens if the central angle of each piece is 1 radian? The general problem: What happens for arbitrary central angles A? Source: Mathematical Mind-Benders by Peter Winkler, published by AK Peters, Wellesley, Mass., 2007, one of the best recent puzzle books I have seen; highly recommended. © Copyright 2008 Stan Wagon. Reproduced with permission. |