Problem of the Week 1088

Star of David

Prove that a Star of David in Pascal's Triangle has the property that the product of the entries in each triangle is the same.

By a Star of David is meant the two small triangles surrounding the binomial coefficient . In this diagram, 15 × 35 × 56 = 20 × 70 × 21.

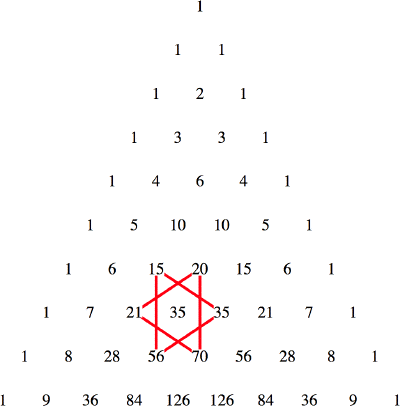
The result, known as the Star of David Theorem, is a variation on this due to H. W. Gould and says that

gcd(, , ) = gcd(, , )

© Copyright 2007 Stan Wagon. Reproduced with permission.