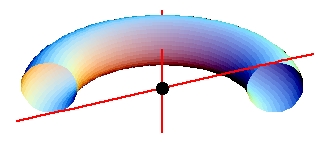
Problem of the Week 997A Strange Way to Slice a DoughnutWhen one slices a doughnut in half in the usual ways, the cross section consists of two circles. This is true when one slices it straight down (the circles are disjoint, and congruent) or through its equatorial plane (the circles are concentric, one inside the other). Consider a torus oriented horizontally with its equatorial plane coinciding with the x-y plane, and its center at (0, 0, 0). In other words, think of a doughnut sitting horizontally on a table, but straddling the x-y plane. Let L be the y-axis. Let M be the line through the origin, lying in the x-z plane, at just the right slope so that it is tangent to the torus in two places; there are two such, but the choice does not matter. So M touches one circle in its upper half, and the other in its lower half. Slice the torus along the plane determined by lines L and M. What is the nature of the curve or curves that form the cross-section? More precisely: Let P be the plane that contains L and M. What exactly is the intersection of P with the torus?
Source: Wolf von Ronik, College Math Journal, 1997 381-383. Also noted in the nice new problem book by Ross Honsberger, Mathematical Diamonds, published by the MAA. © Copyright 2003 Stan Wagon. Reproduced with permission. |