Solution
I received solutions to Problem 1199 from Joseph DeVincentis, Chai Bingqian, and Jay-Calvin Reyes. The proposer, R. Nandakumar, has an elegant approach, which I present below.
The unsolved problem — to accomplish the task with bounded perimeters — generated several solutions, but so far all have been retracted. Nevertheless, there are some good ideas floating around and so it seems that it can be done, and I will post a solution when I receive full details. More details on this problem can be found on Nandakumar's Tech-Musings blog.
Nandakumar's Solution (with extra details by Stan Wagon)
Start with the triangle (0,0), (1,0), (0,1) and form the sequence of triangles of area 1/2, as below:
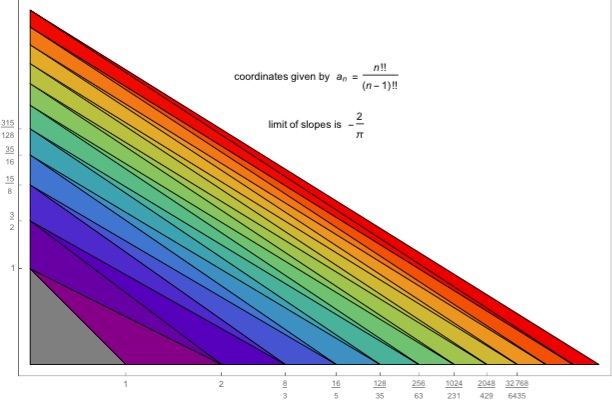
There is a closed form for the coordinates used: a(n) = n!!/(n − 1)!!
The reason is that a(n) = a(n − 2) + (1 / a(n − 1)). If these triangles failed to cover the quadrant, then the coordinates on at least one of the axes would converge. But it is easy to see that a(2n)/2 < a(2n − 1) − a(2n), which implies that they both diverge, since they cannot both converge because of area considerations.
Moreover, the limiting value of the slopes of the lines is -2/π; this is just Wallis's Product for Pi, as the terms of the Wallis product are essentially identical to the slopes, which are n!!² / ( (n − 1)!! (n + 1)!!), where n is even.
It is nice that Mathematica's Limit command, with the appropriate Assumptions (e.g., n is even), can handle limits such as the one mentioned above:
Limit[ (n!!)^2 / ((n - 1)!! (n + 1)!!), n -> Infinity,
Assumptions -> n/2 \[Element] Integers]
Pi / 2
Now, once the first quadrant is done, the others are similar:
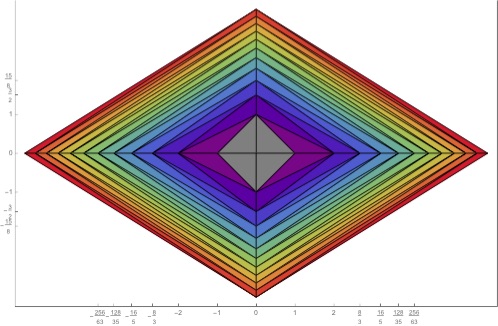
Above, the initial triangles based on points are a small perturbation of the basic triangle in the first quadrant.
Details: For the second quadrant, use a base triangle scaled by q and 1/q, where q is a rational greater than 1, not too far from 1, and not occurring as any of the ratios a[n]/a[m]. That is, use the initial triangle (0,0), (q,0), (0,1/q) (and reflect at the end to move into a different quadrant). This will scale all the coordinates, so they become b[n] = a[n] q on the x-axis and b[n] = a[n]/q on the y-axis.
Now observe that each shortest-side on the x-axis (except from the very first isosceles triangle) is
a[n] − a[n − 2] = 1/a[n − 1]
A new side on the x-axis is
1/b[n − 1] = q (1/a[n − 1])
If this equalled any of the other old sides, then q (1/a[n − 1]) would equal 1/a[m − 1], in contradiction to the definition of q.
Treating the first triangle as a special case, and making a similar argument for the vertical short sides, this implies that none of the new triangles is congruent to any of the old.
To get the third quadrant, choose q′ in the same way that q was chosen, but with q′ different than q. Let c[n] be the corresponding coordinates. Because the ratios of the b-defined sides are the same as for the a-defined sides, none of the c-defined triangles is congruent to an a-triangle or a b-triangle. And the last quadrant is handled the same way.
[Back to Problem 1199]
© Copyright 2015 Stan Wagon. Reproduced with permission.