Problem of the Week 1187
Find the Head-Averse Coin
Solution
Stephen Dupal, Rob Pratt, and Joseph DeVincentis solved the problem.
(Dupal's numbers — 55 and 35 — were a little off; one must be careful about precision issues in the sorts of computations that arise. Mathematica allows high-precision computations with no fuss.)
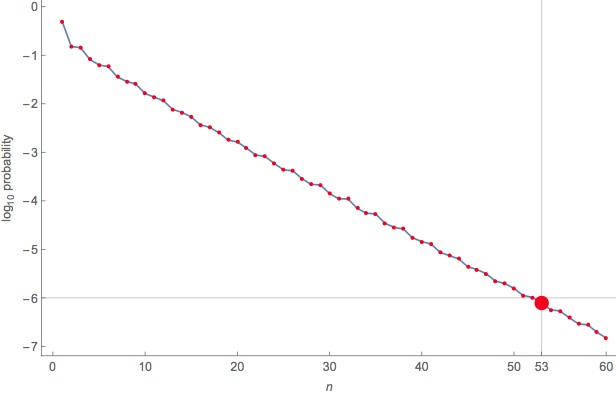
The correct method is: Toss coin C 53 times and if the observed number of heads is 34 or fewer, declare C = A; else, declare C = B. The chance of being wrong is easily computed to be 10-6.107, or just under 1 in a million.
Now, if one can flip both coins in the hope of identifying which is which, as opposed to just one, 52 flips suffice. Throw each coin 26 times for a total of 52. If the head-counts are the same, choose randomly when declaring one to be A (you will be right half the time). Otherwise, choose the one with the smaller head-count to be A. This leads to an error probability of 9.53 × 10-7, or just under one in a million.
Perhaps there is a way of doing this in fewer than 52 flips?
Back to the problem at hand: For given n, one can try various values of the testing condition, i.e., that the number of heads is at most t. The probability of a correct declaration is then:
prob(C = A and C = A is declared) + prob(C = B and C = B is declared)
This is:
1/2 Sum[Binomial[n,i] p^i (1-p)^(n-i), {i,0,t}]
+ 1/2 (1-Sum[Binomial[n,i] q^i (1-q)^(n-i), {i,0,t}])
One can compute this directly, but note that the sums are values of the CDF of the binomial distribution, which Mathematica tells us is the same as the regularized incomplete beta function. So here then is a fast way to compute what is needed, where the output is logarithmic, so that −6 is what is sought.
data[M_] := Table[{test, p = 1/3; q = 9/10;
ans1 = 1/2 BetaRegularized[1-p, M-test, 1+test] ;
ans2 = 1/2 (1-BetaRegularized[1-q, M-test, 1+test]);
N[Log10[ 1 - (ans1 + ans2)]] }, {test, 1, M}];
findTest[M_] := SortBy[data[M], Last] [[1]]
Table[ {n, findTest[n]}, {n, 45, 55}] //Column
{45,{29,-5.3594}}
{46,{30,-5.41713}}
{47,{30,-5.50064}}
{48,{31,-5.65574}}
{49,{32,-5.70357}}
{50,{32,-5.80466}}
{51,{33,-5.95045}}
{52,{34,-5.9886}}
{53,{34,-6.1073}}
{54,{35,-6.24362}}
{55,{36,-6.2723}}
|
The data above shows 53, 34 is the correct (n, t) pair.
Here is a plot of the probability, where t is chosen optimally for n:
[Back to Problem 1187]
© Copyright 2014 Stan Wagon. Reproduced with permission.
|