Solution Notes
Solution to 1183, about 45-degree walks on a x b x c box (Henle walks).
It turns out that the problem in the form I posed it has a very simple solution. Let L denote the number of steps for a "Henle walk" in a box with dimensions a,b,c. Then L(n,1,1)=n, solving the problem as stated. This was first spotted by Nick Baxter, Stephen Meskin, and Joseph DeVincentis. The solution I had in mind was (1,2,1772), which was found by John Guilford and Stephen Morris. J.G. proved it by using the standard trick in such box and billiard problems: unfolding the box into the plane.
And the warmup problem I gave, about the box (√2, π, e), has the surprising answer that L = 5. Computing the exact path is a triviality: it is:
{0, 0, 0} → {√2, √2, 0} → {√2, π, -√2 + π} → {-e + π, π, e} → {0, e, e} → {0, 0, 0}
A box (a,b,c) is called triangular if the sum of any two is greater than or equal to the third; "strictly triangular" is the same, without the "or equal". Any strictly triangular box for which the max is either a or b yields a path of length 5.
There are many nice patterns in this area. Here are some discoveries. The problem seems most natural for the case that a, b, c are integers, though many of the results below hold for reals.
Pictures: A nice way to view the story is to convert (a,b,c) to two numbers by using barycentric coordinates based on an equilateral triangle. That procedure identifies (a, b, c) with (k a, k b, k c), but this irrelevant in this context since L is the same for these. A complex picture shows what the L-set looks like for L running from 1 to 20.
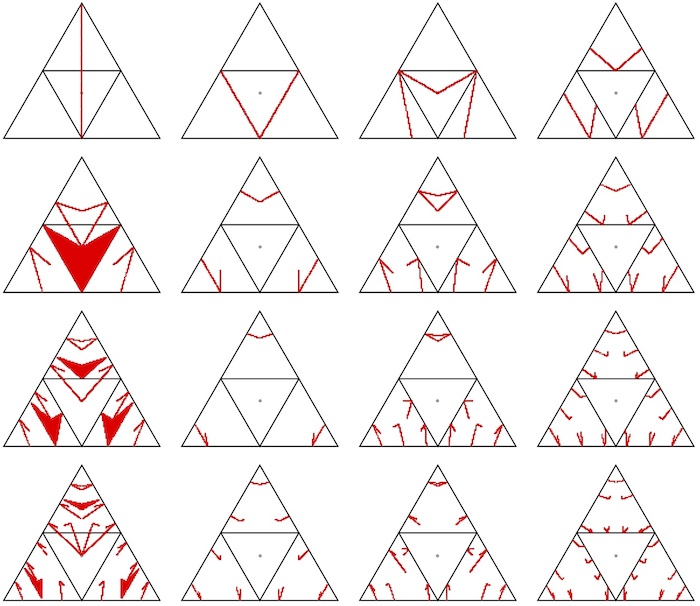
click image to view larger version
For L ≤ 6 there appear to be formulas giving a complete characterization of boxes for which the path length is L (and the diagram above indicates that such formulas, progressively more complicated, exist for all L. Here are some formulas.
Joseph DeVincentis proved these up to n = 5. In the formulas below, we assume that, for box (a,b,c), a ≤ b, since things are symmetric when the first two dimensions are transposed. Here && is "and" and || is "or".
L = 1: a = b
L = 2: b = a + c
L = 3: (b = c && b >= a+1) || (b = 2a+c)
L = 4: (2b = c && b >= a+1) || (b = 2a+2c) || (b =2 a && c <= a-1)
L = 5: a < b && ((b > c && (abc) is strictly triangular) || c = 2 b-a ||
c = 2b+a || b = 2c+3a || (b = 2 c+a && c > a) )
L = 6: b = 3a + 3c || (b = 3 a + c && c < a) || (c = 3 b + a && b > a)
Jim Henle did several good things. He came up with a very efficient algorithm that computes L(a,b,c) (details on request).
Jim also wondered about this variation: Given a box (a,b,c), assume that the triple is strictly triangular and that the three numbers are distinct. Look at the three permutations: (a,b,c), (b,c,a), and (c,a,b). Let i = b - a and j = c - b. Then the sum of the three L-values equals 3 + (8j + 4i) / gcd(i, j). He has proved this formula. He also observes that these triples are "generic" -- they have measure 1 in the space of all triangular boxes.
[Back to Problem 1183]
© Copyright 2014 Stan Wagon. Reproduced with permission.