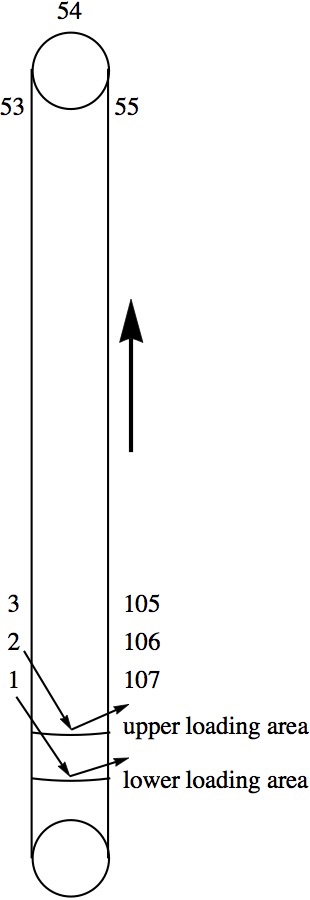
Problem of the Week 1232

The Ski Lift Shuffle

The double-loading six-pack ski lift (by POMA) works like this: There are chairs numbered 1 through N. They go up the mountain in the usual way, making a U-turn at the top. But at the bottom, there are two loading areas, one closer to the top than the other. The first chair down goes to the lower area, while the second one down detaches at the higher loading area. They are both loaded and then they rejoin the main cable so that the second one moves ahead of the first one.

This shows N = 107, the number of chairs in the only such lift in the USA:

Counting up from the bottom in the direction opposite to the motion, and assuming N = 107, we take the initial position indicated above as being

1 2 3 ... 53, then 54 is around the upper wheel.

And descending on the other side, we have

55 56 ... 107.

So when the lift starts up: the descending chairs, counting up from the bottom, are 1, 2, 3, ..., with 1 being the lowest. Then after the first two detachments, chair 2 overtakes chair 1, and the order is

...		...
9		103
8		104
7		105
6		106
5		107
4		2
3		1

Then after the next double detachment, the 4 will overtake the 3 on the upward climb, and so on.

Assuming N chairs, N odd, how many chairs must be loaded so that the initial position will recur for the first time?

Source: Kim Ruhland of Breckenridge, Colorado, who is a ski enthusiast, and my piano teacher. What she really wanted to know was how many times in a day would the lift be in its initial position. To work that out, it helps to know that the loading step for the two chairs takes 12 seconds.

[View the solution]